אתה משתמש בדפדפן מיושן. יתכן והאתר הנוכחי יוצג באופן שגוי, כמו כן אתרים אחרים ברשת.
אנא שדרג את הדפדפן או השתמש בדפדפן חילופי.
אנא שדרג את הדפדפן או השתמש בדפדפן חילופי.
מעגל ומשולש 3
- פותח הנושא עריסטו
- פורסם בתאריך
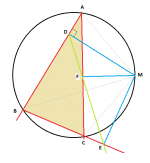
נתון משולש ABC חסום במעגל, נבחר נקודה M על המעגל ונוריד ממנה אנך ל AB בנקודה D ולהמשך BC בנקודה E.
הקטע DE חותך את AC בנקודה F.
צריך להוכיח MF מאונך ל AC כלומר AFM זוית ישרה.
הוכחה:
המרובע DBEM ניתן לחסימה במעגל ( 2 זויות נגדיות ישרות ) , לכן הזויות MBE = MDE כי נשענות על אותה קשת ME במרובע החסום DBEM.
גם הזוויות MBC= MAC שוות נשענות על אותו קשת MC במעגל שחוסם את ABC
לכן MDF = MAF - מהשוויון הזה נובע שגם המרובע ADFM ניתן לחסימה במעגל ( 2 זויות שוות שנשענות על אותו מיתר FM )
במרובע ADFM שניתן לחסימה במעגל הזויות האלו שוות ADM = AFM כי נשענות על אותה קשת AM
ADM היא זוית ישרה לכן גם AFM זוית ישרה, מ.ש.ל.
הקטע DE חותך את AC בנקודה F.
צריך להוכיח MF מאונך ל AC כלומר AFM זוית ישרה.
הוכחה:
המרובע DBEM ניתן לחסימה במעגל ( 2 זויות נגדיות ישרות ) , לכן הזויות MBE = MDE כי נשענות על אותה קשת ME במרובע החסום DBEM.
גם הזוויות MBC= MAC שוות נשענות על אותו קשת MC במעגל שחוסם את ABC
לכן MDF = MAF - מהשוויון הזה נובע שגם המרובע ADFM ניתן לחסימה במעגל ( 2 זויות שוות שנשענות על אותו מיתר FM )
במרובע ADFM שניתן לחסימה במעגל הזויות האלו שוות ADM = AFM כי נשענות על אותה קשת AM
ADM היא זוית ישרה לכן גם AFM זוית ישרה, מ.ש.ל.

נערך לאחרונה ב:
פולגאר
Well-known member
זאת נקודה D ולא A.נבחר נקודה M על המעגל ונוריד ממנה אנך ל AB בנוקדה A
לא, זה נתון לך.צריך להוכיח MF מאונך ל AC כלומר AFM זוית ישרה.
צריך להוכיח שנק' המפגש היא על אותו קו.
נכון התכוונתי D, ותיקנתי בעריכהזאת נקודה D ולא A.
אכן נתון שמורידים אנך מ M ל ACלא, זה נתון לך.
צריך להוכיח שנק' המפגש היא על אותו קו.
אבל אם אני מוכיח ש MF הוא אותו האנך זה מוכיח את הטענה כי הנקודות D F E הם על אותו ישר לפי הבניה.
מעניין מה יש לידידנו ע. לומר על זה.
Lucifer LightBringer
Well-known member
כל הבעיה לא מוגדרת היטב בכלל.נכון!
מעניין מה יש לידידנו ע. לומר על זה.
נקודות לא קיימות בכלל...
עריסטו
Active member
פעם כשמישהו הציג את הפילוסוף/מתמטיקאי/לוגיקן ריימונד סמוליאן לסטודנטים, הוא הציג אותו כך - זהו פרופסור סמוליאן, הוא יוכיח לכם שהוא לא קיים או אתם אינכם קיימים, אבל אתם לא תדעו מה מהשניים.כל הבעיה לא מוגדרת היטב בכלל.
נקודות לא קיימות בכלל...
Copyright©1996-2021,Tapuz Media Ltd. Forum software by XenForo® © 2010-2020 XenForo Ltd.
