בעייה חישובית

[בחשכת הלילה]

משולש שזוויותיו 10°, 50° ו-120° חסום במעגל שרדיוסו שווה 9000 חלקי π.
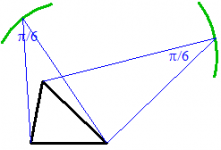
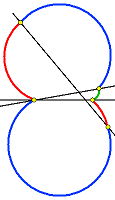
העקומה L היא המקום הגאומטרי של הנקודות המשקיפות על המשולש בזווית 30°.
חשבו את אורכה.

 

[Lucifer LightBringer]

משקיפות?
יש לך שרטוט במקרה?
לא זוכר שבגיאומטריה אנליטית השתמשו במילה הזו.

אתה מתכוון "משתקפות"? יענו reflected?

 

[בחשכת הלילה]

הנה דוגמה לשתי נקודות המשקיפות על משולש בזווית של 30°.
זה לא קשור לגאומטריה אנליטית. זו גאומטריית מישור "רגילה". וקצת טריגונומטריה.
העקומה אמנם רציפה, אבל מורכבת ממספר קשתות שונות. שני חלקים ממנה מוצגים בציור בצבע ירוק.
זו אילוסטרציה בלבד - בציור מוצג משולש אחר.

 

[Lucifer LightBringer]

צפה בקובץ המצורף 137509 הנה דוגמה לשתי נקודות המשקיפות על משולש בזווית של 30°.
זה לא קשור לגאומטריה אנליטית. זו גאומטריית מישור "רגילה". וקצת טריגונומטריה.
העקומה אמנם רציפה, אבל מורכבת ממספר קשתות שונות. שני חלקים ממנה מוצגים בציור בצבע ירוק.
זו אילוסטרציה בלבד - בציור מוצג משולש אחר.

תראה כשלמדתי בתיכון, דיברו על מקום גיאומטרי (locus) בשיעורים על גיאומטריה אנליטית.
לא דיברנו בכלל על מקום גיאומטרי בגיאומטריה אוקלידית וטריגו.
(גם לא היו שאלות של בנייה עם סרגל ומחוגה, למרות שהן מופיעות בחלק מהספרים.
דרך אגב בתמונה השנייה הקטע הירוק צריך להיות גם אדום, לא?


בנוגע לשאלה שלך, אני מנסה לחשוב איך לתרגם אותה (מתברר שצ'אטי בוט מעדיף אנגלית על פני עברית... go figure.
בכל מקרה אם תרגמתי את זה כמו שצריך זה יוצא משהו כזה: sqrt(6)+sqrt(2))*18000).

למרות שזה נקרא לרמות בימינו...

דרך אגב, אני נזכר באתר מאוד חביב:

Interactive Mathematics Miscellany <br>and Puzzles

www.cut-the-knot.org

 

[בחשכת הלילה]

GPT לא מסתדר עם התרגיל הזה אין טעם לשאול אותו.
לכל צלע של המשולש יכולות להיות מקסימום שתי קשתות המשקיפות עליה בזווית 30° - משני הצדדים! שתי קשתות בעלות אותו צבע בציור, משקיפות על אותה צלע.
הקשת הקטנה הירוקה נשארה בלי "בת זוג".
שתי הקשתות הכחולות משקיפות על הצלע שמול זווית 120°. שתי הקשתות האדומות - על הצלע מול זווית 50°. הקשת הירוקה - על הצלע מול זווית 10°.
לכל גדלי הקשתות יש נוסחאות ממש לא מסובכות.

 

[Lucifer LightBringer]

GPT לא מסתדר עם התרגיל הזה אין טעם לשאול אותו.
לכל צלע של המשולש יכולות להיות מקסימום שתי קשתות המשקיפות עליה בזווית 30° - משני הצדדים! שתי קשתות בעלות אותו צבע בציור, משקיפות על אותה צלע.
הקשת הקטנה הירוקה נשארה בלי "בת זוג".
שתי הקשתות הכחולות משקיפות על הצלע שמול זווית 120°. שתי הקשתות האדומות - על הצלע מול זווית 50°. הקשת הירוקה - על הצלע מול זווית 10°.
לכל גדלי הקשתות יש נוסחאות ממש לא מסובכות.

אכן יש נוסחא לחישוב אורך קשתות. כאשר הזווית המרכזית נתונה אז אורך הקשת שווה ל- 2Pi*R*alpha/360.

אבל לא ברור מהדוגמא הראשונה היא איך אתה מעביר שני קווים ישרים מקודקוד שעל הקשתות. (הדוגמא עם הזווית 30 מעלות.)

האם זו בעיה עם סרגל ומחוגה?
אני גרוע בזה.

 

[בחשכת הלילה]

אכן יש נוסחא לחישוב אורך קשתות. כאשר הזווית המרכזית נתונה אז אורך הקשת שווה ל- 2Pi*R*alpha/360.

אבל לא ברור מהדוגמא הראשונה היא איך אתה מעביר שני קווים ישרים מקודקוד שעל הקשתות. (הדוגמא עם הזווית 30 מעלות.)

האם זו בעיה עם סרגל ומחוגה?
אני גרוע בזה.

רצית לשאול, איך אני מוצא את מרכזי המעגלים של הקשתות, ואת זוויותיהן. להעביר קטע בין שתי נקודות נתונות, אני מניח שאתה יודע
רמז: מרכז המעגל של קשת משקיף על הצלע, שעליה הקשת נשענת, בזווית של 60°. ואז כל נקודה על הקשת (מאותו הצד של הצלע הנתונה!) תשקיף על אותה צלע בזווית של 30°.
זה גם אומר לך לנו את הערכים של כל ה-R-ים.

 

[בחשכת הלילה]

והנה ציור של המשולש "שלנו" והעקומה שלו:

 

[בחשכת הלילה]

מצורף קובץ פתרון כללי.

 

[Lucifer LightBringer]

מצורף קובץ פתרון כללי.

יש את המשפט הזה שזווית מרכזית שווה לפעמיים זווית היקפית.
לא חשבתי על זה בכלל, מתי הפעם האחרונה שהשתמשתי במשפט הזה?!